SVM optimization based on machine learning algorithm

Machine learning will definitely design algorithm optimization problems, mainly to implement Platt SMO algorithm. Then, the following article introduces the optimization of SVM, mainly realizes Platt SMO algorithm optimization SVM model, and tries to use genetic algorithm framework GAFT to initial SVM. Optimized.

Heuristic selection variable in SMO

In the SMO algorithm, we need to select a pair of α to optimize each time. Through heuristic selection, we can more efficiently select the variables to be optimized so that the objective function drops the fastest.

Different heuristics are taken for the first α1 and the second α2 Platt SMO.

Selection of the first variable

The choice of the first variable is an outer loop, which is different from the previous convenience of the entire αα list, where we alternate between the entire sample set and the non-boundary sample set:

First, we traverse the entire training set to check whether it violates the KKT condition. If the changed αiαi and xi, yixi, yi violate the KKT condition, the change point needs to be optimized.

The Karush-Kuhn-Tucker (KKT) condition is a sufficient and necessary condition for the most advantageous of the positive definite quadratic programming problem. For the SVM dual problem, the KKT condition is very simple:

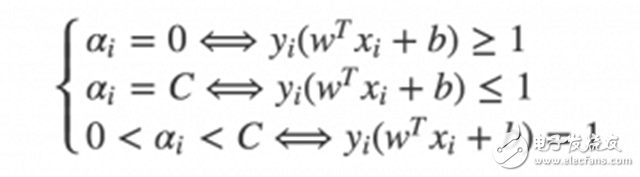
After traversing the entire training set and optimizing the corresponding α, we only need to traverse the non-boundary α in the second iteration. The so-called non-boundary α refers to those alpha values ​​that are not equal to the boundary 0 or C. Again, these points still need to be checked for violations of KKT conditions and optimized.

After that, it is constantly alternating between the two data sets. When all the αs satisfy the KKT condition, the algorithm is aborted.

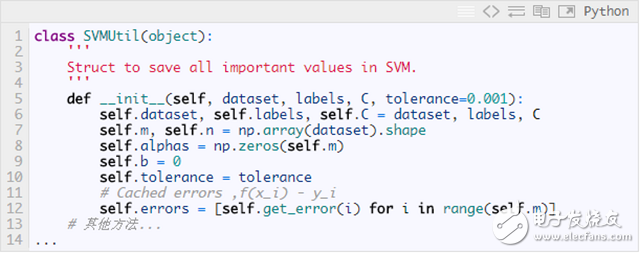
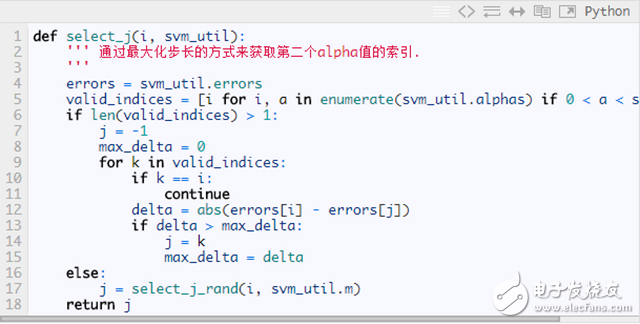
In order to be able to quickly select α with the largest step size, we need to cache the error corresponding to all data, so we specially wrote a SVMUTIl class to save the important variables in svm and some auxiliary methods:

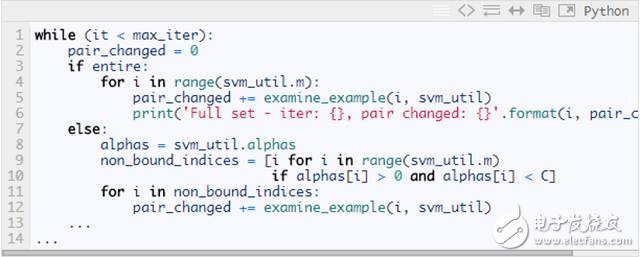
Let's select the approximate code for the alternate traversal of the first variable, the corresponding complete Python implementation (see https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py for a complete implementation):

The choice of the second variable

The selection process of the second variable in SMO is an inner loop. When we have selected the first α1, we hope that the second variable α2 we selected can be greatly changed after optimization. According to our previous derivation

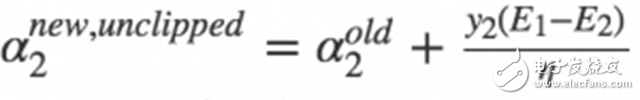
It can be known that the new α2 change depends on |E1−E2|, when E1 is positive, then the smallest Ei is selected as E2, and the Ei of each sample is usually buffered into a list, by selecting in the list with | The α2 of E1−E2| is approximately the maximum step size.

Sometimes the function values ​​that are still not able to follow the above heuristics are sufficiently degraded. This is done by the following steps:

Select a sample on the non-boundary data set that will cause the function value to drop enough as the second variable

If there is no on the non-boundary data set, then the second variable is selected only on the entire data.

If not still, reselect the first α1

The second variable is chosen for the Python implementation:

KKT conditions allow for certain errors

In the judgment of the KKT condition in the Platt paper, there is a tolerance that allows a certain error, the corresponding Python implementation:

See the full implementation of Platt SMO at: https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py

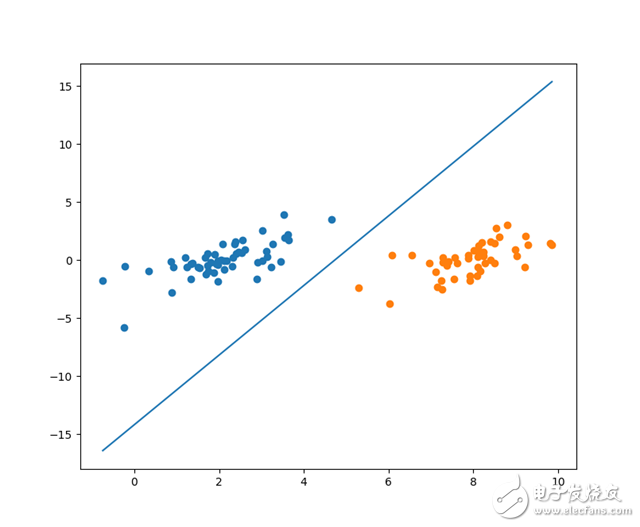
For the previous data set we optimized using Platt SMO to get:

Visualize split lines and support vectors:

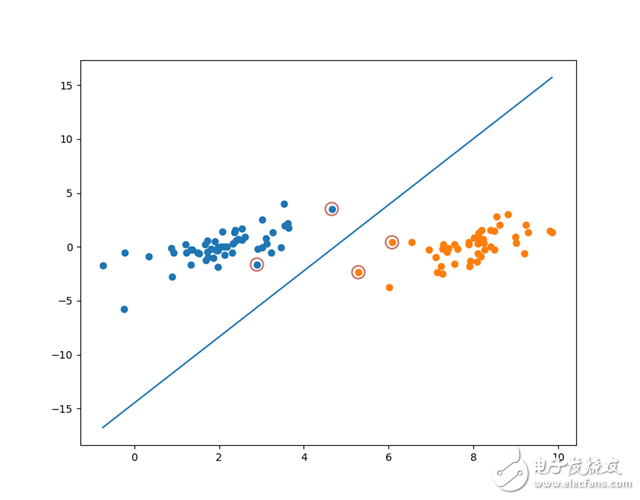
It can be seen that the support vector optimized by Platt SMO is slightly different from the simplified version of the SMO algorithm.

Optimize SVM using genetic algorithms

Since I recently wrote a genetic algorithm framework, genetic algorithm is very easy to use as a heuristic non-guided search algorithm, so I tried to use genetic algorithm to optimize SVM.

Using genetic algorithm optimization, we can directly optimize the original form of SVM, which is the most intuitive form:

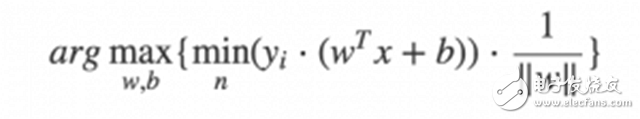
By the way, Amway's own genetic algorithm framework, with the help of this framework, we only need to write dozens of lines of Python code to optimize the SVM algorithm. The most important one is to write the fitness function. According to the above formula, we need to calculate the distance from each point in the dataset to the dividing line and return the minimum distance, and then put it into the genetic algorithm for evolutionary iteration.

The genetic algorithm framework GAFT project address: https://github.com/PytLab/gaft, please refer to the README for details.

Ok, we started building populations for evolutionary iterations.

Create individuals and populations

For two-dimensional data points, we need to optimize only three parameters, namely [w1, w2] and b. The individual definitions are as follows:

The population size is taken here to create a population.

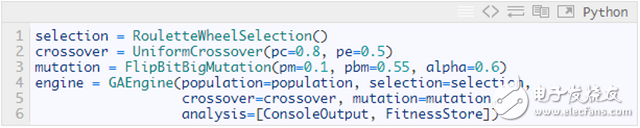
Create genetic operators and GA engines

There is nothing special here, just use the built-in operator in the framework.

Fitness function

This part just needs to describe the initial form of svm above, just three lines of code:

Start iteration

Iterate 300 generations of population here

Draw a genetic algorithm optimized partition line

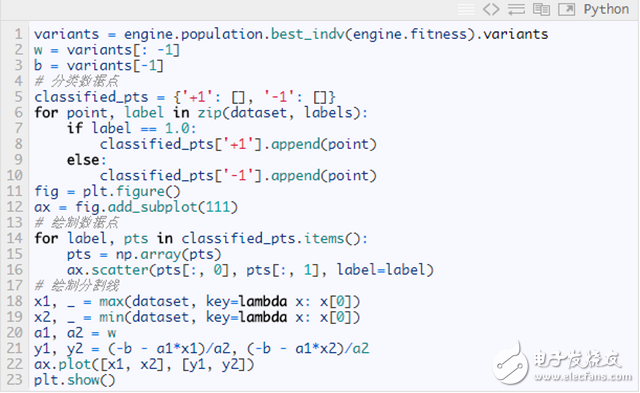
The resulting segmentation curve is shown below:

Bottle Camera

Micro camera is the product of modern high-tech, also known as micro monitor, which has the characteristics of small size, powerful function and good concealment.

Micro cameras are widely used, suitable for aviation, commerce, media, enterprises and institutions, families and other industries. The emergence of miniature cameras brings convenience to people's lives, and at the same time, some phenomena related to corporate secrets and personal privacy also arise.

Bottle Camera,Spy Hidden Camera,Micro camera

Jingjiang Gisen Technology Co.,Ltd , https://www.gisentech.com